The ppm-mineralogy (©NATI Research) is the technology, the aim of which is to calculate the weight and correctly process the representative sample until the analytical subsample for further mineralogical, isotopic, chemical and etc. studies. Sample processing part of the Technology is being carried out with predictable and calculable losses and with saving of all the sample properties for reaching the aim of the study. The technology comprises the theoretical metrological and the practical instrumental elements in order to obtain the utilitarian result, witch fulfill the purpose of the study or work.

Representative sample weight calculation.

The term representative sample here and after is understood as the minimum weight of the sample, which has same commodity element mass concentration (concentration in further text) as in the whole object of study. The concentration is the relation of the component mass to the total mass of a mixture. It means that it is just a digit, which has no physical meaning. Then, how the representative weight of the sample could be calculated from the digit? In our Company we found the solution, which based on the phase (material) conceptual approach.

Following the definition of the term concentration of some chemical element in a rock “C” distributed into “n” amount of various minerals the next expression will be right:

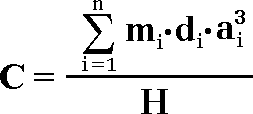
               [ 1 ]

Where the numerator expresses the total mass of the chemical element of interest distributed in “n” number of grains, when each i^th grain has density “d”, volume “a³” (cubic shape approximation) and element concentration in the grain “m”; whereas the denominator shows the whole sample mass H. Strictly speaking, the real volume of each i^th grain “V” should be used in formula, instead of “a³”. However, due to the fact that volume of each single grain is a function of its shape, with different mathematical approximations, in present case the simplest for understanding way of approximation is used – grain shapes are approximated as cubes with edge “a”.

The above formula [1] describes an ideal case, when “n” amount of different mineral grains are distributed in the mixture. However, the real practice shows that not always all the occurring grains of interest are being extracted into analytical subsample. It become necessary to take into account a concept of extraction factor “I”, which shows the amount of the extracted grains “n” in reference to the amount of really occurring grains “n'”: Then, the formula [1] becomes like:

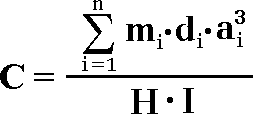
            [  2  ]

The formula theoretically grounds the notion concentration. However, there is still a question how to apply that to the representative sample weight calculation before the study, when the variables are unknown? Then, the aim of the study, together with common sense and logics are coming to help.

The variables “m” and “d” are obvious when the aim of the study is formulated. In other words, the aim grounds what mineral or minerals we are interested in. Then, “C” and “a” will be set up according to common sense – that are the lowest concentration and biggest grain size, which would have sense for the present study. In other words, that are the lowest concentration of the commodity element, below which the study does not make sense to be done (it would not answer the aim of the study); and biggest grain size of the commodity phase (mineral), which is reasonably possible in the sample for the study (the biggest grain, which theoretically and empirically possible to occur in the sample). The amount of commodity grains “n” grounds simply – it usually sets up as 1. It means that the study is interested at least in one grain. One grain is minimum sufficient amount to reach the aim of study (the more grains the more information by the end of the study). Value “I” is dictated by the accuracy of the processing flow sheet and the equipment. It means how correctly the sample will be processed until the analytical subsample.

In the sense of said above the parameter “C” becomes understood not as “concentration”, but as “work sensitivity”. Obviously, that work sensitivity is totally different from the analytical equipment sensitivity. As well, comprising all above, before each study starts some ultimate values of the parameters have to be setup in accordance to the peculiarity and the aim of the study.

Correct representative sample processing.

Usually, in practice of work, the representative sample is way bigger than the analytical subsample. Independently from the analytical subsample type (5g sand for chemical analyses or monolayer microscope specimen, or else), the sample processing must be done in accordance to the aim of the study and under strict metrological rules, which ensure the correctness of the processing and losses calculation. All existing sample processing equipment has known accuracy and precision. However, there are cases, when conventional equipment has insufficient sensitivity for some phases with particular chemical and physical properties. In other words, in some cases, the losses are either incalculable (unpredictable) or the losses are reaching 100%. In both cases the interpretation of the results are impossible and do not have any sense to be done.

Such difficulties often occur in research, prospecting, exploration and mineral processing works, especially when the deal is going on with small (up to 50µm) rarely distributed grains of precious metals or high-tech metals, or minerals for isotopic studies.

In order to solve the problem, new equipment “Makharay 3” had been invented and developed in NATI Research JSC (patented by "NATI" Research JSC, 1996, Russia). The equipment is based on gravity hydro-separation and allow the enrichment into concentrate of phases with density more than 5-6g/cm³ with grain size at first or first tens of µm and concentration factor (CF in further text) of 10² – 10⁶ times. As well, the concentrator allows collecting of different pre-products. For example, in case of gold studies, the pre-concentrate will be composed of “heavy” sulfides or/and sulfarsenides; and the pre-pre-concentrate will consist of mainly magnetite-chromite minerals.

The accuracy of the equipment is different for different minerals and different matrixes. One of the accuracy examples is shown on the graph below. The graph shows dependence of the losses (concentrator accuracy “I”, see formula [2]) from the CF for different gold grain sizes in 3-4g/cm³ sand matrix, below 250µm size fraction.

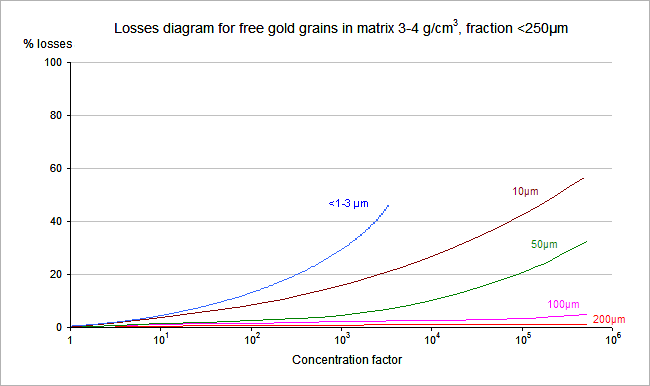
As it clear from the graph, the value “I” of the Makharay3 in case of working with the gold grain in 10µm with CF = 10⁵ is around 60% (only 40% of losses). No other existing equipment could provide such high accuracy. Not even the illegal copy of NATI’s old prototype equipment, which is now on the market under the name HS-0x, made by Rudashevsky/Cabri.